Uspořádané dvojice
Definice (Uspořádaná dvojice).
Nechť \(x,y\) jsou dvě množiny. Uspořádanou dvojicí \(⟨x,y⟩\), jejíž
**první komponentou** je množina \(x\) a **druhou komponentou** je
množina \(y\), rozumíme množinu \[ ⟨x,y⟩ = \{\{x\}, \{x,y\}\}. \]
Věta
Nechť \(u,v,x,y\) jsou dané množiny. Potom \[ ⟨x,y⟩ = ⟨u,v⟩ ⇔ x = u ∧
y = v. \]
Důkaz.
Důkaz proveďte jako samostatné cvičení.\(\square\)
Věta.
Nechť \(A,B\) jsou množiny. Pro všechna \(x ∈ A\) a pro všechna \(y ∈
B\) platí: \(⟨x,y⟩ ∈ P(P(A∪B)).\)
Důkaz.
Nechť \(x ∈ A\) a \(y ∈ B.\) Potom zřejmě z definice potenční množiny
plyne \(\{x\}, \{x,y\} ∈ P(A ∪ B).\) Tedy \(\{\{x\}, \{x,y\}\} ⊆ P(A ∪
B).\) Pak \(\{\{x\}, \{x,y\}\} ∈ P(P(A ∪ B)).\) Tedy dokázali jsme, že
pro každé \(x ∈ A\) a \(y \in B\) je \(⟨x,y⟩ ∈ P(P(A ∪ B)).\) \(\Box\)
Definice (Kartézský součin).
Jsou-li \(A,B\) dané množiny, potom
kartézským součinem množin \(A,B\) budeme rozumět jednoznačně
určenou množinu \[ A×B = \{⟨x,y⟩ ∈ P(P(A ∪ B)): x ∈ A ∧ y ∈ B\}. \]
Příklad.
Nechť \(A = \{2,3\}\) a \(B = \{a,b,c, 3\}\). Potom \[ A×B = \{⟨2,a⟩,
⟨2,b⟩, ⟨2,c⟩, ⟨2,3⟩, ⟨3,a⟩, ⟨3,b⟩, ⟨3,c⟩, ⟨3,3⟩\}. \]
Relace
Definice (Relace).
(Binární) relací \(R\) rozumíme jakouko-li množinu, jejímiž
elementy jsou uspořádané dvojice.
Definice.
Nechť \(A,B\) jsou dané množiny.
Binární relací mezi množinou \(A\) a \(B\) se rozumí
libovolná podmnožina \(R\) kartézského součinu \(A×B\), tj. \(R⊆A×B.\)
Definice (Relace na množině).
Nechť \(A\) je množina. Množina \(R\) se nazývá
(binární) relací na množině \(A\) , je-li \(R⊆A×A.\)
Lemma.
Nechť \(R\) je binární relace a nechť pro \(x\) existuje \(y\) tak, že
\(⟨x,y⟩∈R.\) Potom \(x ∈ ⋃⋃R.\)
Lemma.
Nechť \(R\) je binární relace a pro \(y\) existuje \(x\) tak, že
\(⟨x,y⟩ ∈ R.\) Potom \(y∈⋃⋃R.\)
Definice.
Předpokládejme, že \(R\) je binární relace.
1. Definičním oborem
relace budeme rozumět množinu \[ dom (R) = \{x ∈ ⋃⋃R: ∃y(⟨x,y⟩ ∈ R)\}.
\]
2. Oborem hodnot relace \(R\) budeme rozumět množinu \[
ran (R) = \{y ∈ ⋃⋃R: ∃x(⟨x,y⟩ ∈ R)\}. \]
3. Polem relace
\(R\) budeme rozumět množinu \[ fld(R) = dom(R) ∪ ran(R). \]
Funkce
Definice
Řekneme, že binární relace \(R\) je jednoznačná, jestliže pro
každé \(x ∈ dom(R)\) existuje právě jedno \(y\) takové, že \(⟨x,y⟩ ∈
R.\) Tedy z toho, že zároveň platí \(⟨x,y⟩ ∈ R\) a \(⟨x,z⟩ ∈ R\),
plyne \(y = z.\)
Definice.
Funkcí budeme rozumět binární relaci \(F,\) která je
jednoznačná. To znamená, že pro každé \(x ∈ dom(F)\) existuje právě
jedno \(y\) takové, že \(⟨x,y⟩ ∈ F.\)
Definice.
Nechť \(A\) a \(B\) jsou množiny a nechť \(F\) je relace mezi
množinami \(A\) a \(B\). Řekneme, že \(F\) je
funkce množiny \(A\) do množiny \(B\) a píšeme \(F:A \to B,\)
pokud platí:
1. \(dom(F) = A,\)
2. \(F\) je jednoznačná relace. Množinu \(dom(F)\) nazveme definičním
oborem funkce \(F\).
3. \(ran(F) ⊆ B.\)
Příklad.
Nechť \(A = \{a,b,c,d,e\}\) a \(B = \{5,6,7,8,9\}\). Dále položme \(F
= \{⟨a, 8⟩, ⟨b,7⟩, ⟨c,9⟩, ⟨d,6⟩, ⟨e,5⟩\}\). Potom je \(F\) funkce
množiny \(A\) do množiny \(B\), tj. \(F:A \to B\). Na druhé straně
binární relace \(G\) definovaná \[ G = \{⟨a,8⟩, ⟨b,7⟩, ⟨c,9⟩, ⟨d,6⟩,
⟨b,8⟩, ⟨e,5⟩\} \] není funkcí množiny \(A\) do množiny \(B\). To
proto, že \(⟨b, 7⟩ ∈ G\) a zároveň \(⟨b, 8⟩ ∈ G\), ale \(7 \neq 8.\)
Příklad.
Nechť \(A = \{a,b,c,d\}\) a \(B = \{1,2,3,4,5\}\). Uvažujme funkci
\(F:A \to B\) definovanou výčtem prvků: \(F = \{⟨a,3⟩, ⟨b,5⟩, ⟨c,1⟩,
⟨d,3⟩\}\). Potom je \[ F(a) = 3, F(b) = 5, F(c) = 1, F(d) = 3. \]
Definice.
Nechť \(A,B\) jsou množiny. Potom definujme třídu všech funkcí množiny
\(A\) do množiny \(B\) jako třídu \[ B^A = \{F: F \text{ je funkcí
množiny } A \text{ do množiny } B\}. \]
Operace s funkcemi
Definice.
Nechť \(F\) a \(G\) jsou funkce.
1. Inverzí funkce \(F\) budeme rozumět binární relaci \[
F^{-1} = \{⟨v,u⟩: ⟨u,v⟩ ∈ F\}. \] Tudíž \(⟨y,x⟩ ∈ F^{-1} ⇔ ⟨x,y⟩ ∈ F
⇔ F(x) = y.\)
2. Je-li \(A\) množina, potom restrikcí funkce \(F\) na
množinu \(A\) se rozumí funkce \[ F↾A = \{⟨u,v⟩: ⟨u,v⟩ ∈ F ∧ u ∈ A\}
\] jejíž definičním oborem je množina \(dom(F) ∩ A.\)
3. Pro libovolnou množinu \(A ⊆ dom(F)\) definujeme
obraz množiny \(A\) vzhledem k funkci \(F\) jako podmnožinu
množiny \(ran(F)\) definovanou vztahem \[ F[A] = \{F(x):x ∈ A\} =
\{y: ∃x(x ∈ A ∧ y = F(x))\}. \]
4. Je-li \(B\) množina, potom definujeme
úplný vzor množiny \(B\) vzhledem k funkci \(F\) jako
podmnožinu množiny \(dom(F)\) danou vztahem \[ F^{-1}[B] = \{u ∈
dom(F): F(u) ∈ B\}. \]
5. Jsou-li \(F\) a \(G\) dvě funkce, potom definujeme jejich
složení (kompozici) \(F\circ G\) jako množinu: \[ F\circ G =
\{⟨u,v⟩: \exists t(⟨u,t⟩ ∈ G ∧ ⟨t,v⟩ ∈ F)\}. \] Jinak řečeno,
\(⟨u,v⟩ ∈ F ∘ G ⇔ ∃t(⟨u,t⟩ ∈ G ∧ ⟨t,v⟩ ∈ F).\)
Poznámky.
(a) Je-li \(F\) funkce, potom je obecně vzato inverze \(F^{-1}\)
binární relace, která nemusí být funkcí.
(b) Je-li \(F\) funkce a \(A ⊆ dom(F),\) potom \(F↾A : A \to
ran(F).\)
(c) Jsou-li \(F\) a \(G\) dvě funkce, proto jejich kompozice \(F∘G\)
je též funkce.
(d) Je-li \(F:A \to B\) funkce, potom je obor hodnot (range angl.)
množina, kterou lze definovat zápisem \[ F[A] = \{F(x): x ∈ dom(F)\}
\] neboť \(F\) je jednoznačnou relací.
Věta.
Nechť \(F\) a \(G\) jsou funkce. Potom platí
(a) \(F∘G\) je funkce.
(b) \(dom(F∘G) = \{x ∈ dom(G): G(x) ∈ dom(F)\}.\)
(c) Pro všechna \(x ∈ dom(F ∘ G)\) máme \((F \circ G)(x) =
F(G(x)).\)
Prosté funkce
Definice.
Funkce \(F\) se nazývá prostá, jestliže pro každé \(x,y ∈
dom(F)\) platí: \[ F(x) = F(y) ⇒ x = y. \]
Definice.
Funkce \(F\) se nazývá surjekce, jestliže pro každé \(y ∈
ran(F)\) existuje \(x ∈ dom(F)\) takové, že \(F(x) = y.\) Formálně:
\[ ∀y ∈ ran(F) ∃x ∈ dom(F): F(x) = y. \] Jinak, pokud \(F:A \to B,\)
pak \(F\) je surjekce, právě když \(ran(F) = B.\) Opět formálně: \[
(∀y ∈ B)(∃x ∈ A): F(x) = y. \]
Definice.
Funkce \(F\) se nazývá bijekce, jestliže je prostá a je
surjekcí. Jinak řečeno, \(F\) je bijekce, právě když pro každé \(y ∈
ran(F)\) existuje právě jedno \(x ∈ dom(F)\) takové, že \(F(x) =
y.\) Formálně: \[ (∀y ∈ ran(F))(∃!x ∈ dom(F)): F(x) = y. \]
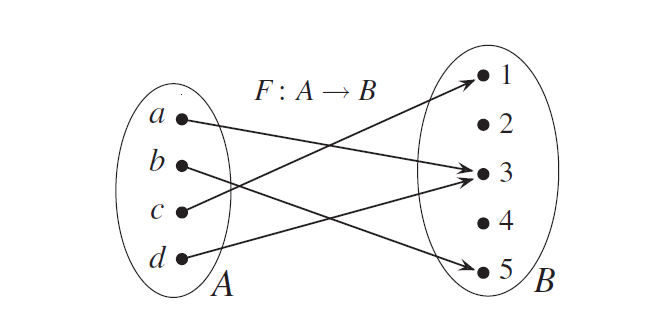
Následující obrázek ukazuje diagram, který znázorňuje prostou funkci
\(F:A \to B\), která není surjekcí.
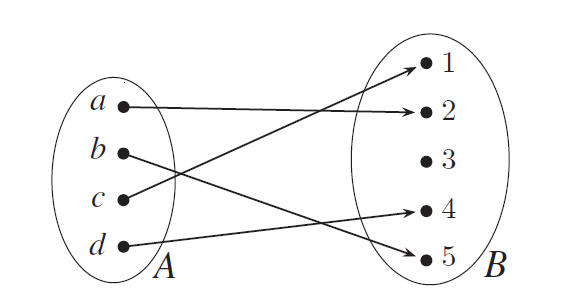
Na dalším obrázku je znázorněna funkce \(F:A \to B\), která je
surjekcí, ale není prostá.
Věta.
Jsou-li funkce \(g:A \to B\) a \(f:B \to C\) prosté, potom jejich
kompozice \((f∘g): A \to C\) je též prostou funkcí.
Relace uspořádání
Definice.
Binární relace \(R\) se nazývá antisymetrická, jestliže pro
každé \(x,y\) platí: \[ ⟨x,y⟩ ∈ R ∧ ⟨y,x⟩ ∈ R ⇒ x = y. \]
Definice.
Binární relace \(≼\) na množině \(A\) se nazývá
částečným uspořádáním množiny \(A\) , jsou-li pro všechna
\(x,y,z ∈ A\) splněny podmínky:
1. \(x ≼ x.\) (reflexivita)
2. Jestliže \(x ≼ y\) a \(y ≼ x,\) potom \(x = y.\) (antisymetrie)
3. Jestliže \(x ≼ y\) a \(y ≼ z,\) potom \(x ≼ z.\) (tranzitivita)
Uspořádanou dvojici \((A, ≼)\) pak nazveme
částečně uspořádanou množinou.
Příklad.
Uvažujme neprázdnou množinu \(\mathcal F\) a nechť \(≼\) je binární
relací na \(\mathcal F\) definovaná takto \[ (∀U,V∈\mathcal F)(U ≼ V ⇔
U ⊆ V). \] Potom je relace \(≼\) částečným uspořádáním množiny
\(\mathcal F.\) Toto tvrzení splňuje všechny tři požadavky částečného
uspořádání:
1. Reflexivita: Pro každé \(U ∈ \mathcal F\), \(U ⊆ U\), což znamená,
že \(U ≼ U\).
2. Antisymetrie: Jestliže \(U ≼ V\) a \(V ≼ U\), pak \(U ⊆ V\) a \(V ⊆
U\), což implikuje \(U = V\).
3. Tranzitivita: Jestliže \(U ≼ V\) a \(V ≼ W\), pak \(U ⊆ V\) a \(V ⊆
W\), což implikuje \(U ⊆ W\), tedy \(U ≼ W\).
Takže relace \(≼\) skutečně tvoří částečné uspořádání na množině
\(\mathcal F\).
Definice.
Předpokládejme, že \(≼\) je částečným uspořádáním množiny \(A\).
Relace \(≼\) se pak nazve
úplným (lineárním uspořádáním) množiny \(A\), jestliže je
splněna podmínka \[ (∀x ∈ A)(∀y ∈ A)(x ≼ y ∨ y ≼ x). \] Uspořádanou
dvojici \((A, ≼)\) pak nazveme úplně uspořádanou množinou.
Příklad.
\((\mathbb R, \le)\) je úplně uspořádaná množina.
Definice.
Nechť \((A,≼)\) je částečně uspořádanou množinou. Pro \(x,y ∈ A\)
definujeme \(x ≺ y\) právě tehdy, když \(x ≼ y\) a zároveň \(x \neq
y.\) Relaci \(≺\) na množině \(A\) nazveme
striktním uspořádáním
odpovídajícím uspořádání \(≼.\)
Poznámka.
Je-li \((A,≼)\) úplně uspořádaná množina, potom odpovídající striktní
uspořádání \(≺\) splňuje tzv. trichotomii na množině \(A\): pro
každé dva elementy \(x\) a \(y\) množiny \(A\) platí právě jedna z
následujících podmínek: \(x ≺ y,\) \(x = y,\) \(y ≺ x.\)
Definice.
Nechť je \((A,≼)\) částečně uspořádanou množinou a nechť \(S ⊆ A,\)
\(a ∈ A\) a \(b ∈ A.\)
1. Jestliže \((∀x ∈ S)(x ≼ b)\) a \(b ∈ S\),
potom element \(b\) nazýváme největším elementem množiny \(S.\)
2.
Jestliže \((∀x ∈ S)(a ≼ x)\) a \(a ∈ S\), potom element \(a\) nazveme
*nejmenším elementem množiny \(S.\)