Určité integrály

Problém výpočtu obsahu

Uvažujme rovinný obrazec $S$, který je zobrazen na obrázku a jehož obrázek vidíme dole.

Nyní rozdělme obrazec na částí pomocí vertikálních přímek $x = \frac{1}{4}, x = \frac{1}{2}, x = \frac{3}{4}.$ Viz obrázek níže.

Dále každý křivočarý lichoběžník $S_1, S_2, S_3$ a $S_4$ nahraďme obdélníkem jak ukazuje následující obrázek.

Interval jsme rozdělili na čtyři intervaly o stejné délce: $⟨0, \frac{1}{4}⟩,\ ⟨\frac{1}{4}, \frac{1}{2}⟩,\ ⟨\frac{1}{2},\frac{3}{4}⟩$ a $⟨\frac{3}{4},1⟩.$ Výška každého obdélníka, který aproximuje obrazec $S_i$ je rovna funkční hodnotě funkce $f(x)$ v pravém koncovém bodě příslušného dílčího intervalu tvořícího základnu obdélníka. Tedy každý z těchto obdélníků má šířku $\frac{1}{4}$ a výšky jsou postupně rovny $\left(\frac{1}{4}\right),\ \left(\frac{1}{2}\right),\ \left(\frac{3}{4}\right)$ a $1^2.$ Nechť $R_4$ označuje součet obsahů jednotlivých obdélníků, tedy \[ R_4 = \frac{1}{4}\cdot\left(\frac{1}{4}\right)^2 + \frac{1}{4}\cdot\left(\frac{1}{2}\right)^2 + \frac{1}{4}\cdot\left(\frac{3}{4}\right)^2 + \frac{1}{4}\cdot(1)^2 = \frac{15}{32}. \] Z obrázku nahoře je zřemé, že obsah $A$ obrazce $S$ je menší než $R_4,$ tedy $$ A < \frac{15}{32}. $$ Nyní aproximujme obrazec $S$ pomocí obdélníků, jejichž výška bude tentokrát rovna funkční hodnotě funkce $f(x) = x^2$ v levém koncovém bodě každého dílčího intervalu $⟨0, \frac{1}{4}⟩,\ ⟨\frac{1}{4}, \frac{1}{2}⟩,\ ⟨\frac{1}{2},\frac{3}{4}⟩$ a $⟨\frac{3}{4},1⟩.$ Viz následující obrázek:

Součet obsahů jednotlivých aproximujících obdélníků je analogicky roven: $$ L_4 = \frac{1}{4} \cdot 0^2 + \frac{1}{4} \cdot \left(\frac{1}{4}\right)^2 + \frac{1}{4} \cdot \left(\frac{1}{2}\right)^2 + \frac{1}{4} \cdot \left(\frac{3}{4}\right)^2 = \frac{7}{32}. $$ Takto jsme dostali dolní odhad obsahu obrazce $S.$ Platí: $$ \frac{7}{32} < A < \frac{15}{32}. $$ Je samozřejmě možné zopakovat výpočet pro jemnější aproximaci obrazce pomocí více dílčích intervalů. Například, pokud zdvojnásobíme počet aproximujících obdélníků, dosataneme odhady: $$ 0.2734375 < A < 0.3984375 $$ Ještě přesnější odhady dostaneme postupným zvětšováním počtu aproximujících obdélníků. Viz následující tabulka:

Na následujícím obrázku vidíte aproximaci obrazce pro počet $n = 8.$

Ukažme dále, že pro $n \to \infty$ posloupnost $(R_n)$ konverguje a platí: $$ \lim_{n \to \infty} R_n = \frac{1}{3}. $$ K výpočtu použijeme vzorec pro výpočet součtu kvadrátů prvních $n$ přirozených čísel: $$ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}. $$ $R_n$ bude označovat součet obsahů obdélníků, které tvoří horní aproximaci obrazce $S$ a výška každého obdélníku bude rovna funkční hodnotě funkce $f(x) = x^2$ v pravém koncovém bodě.

Tedy $$ \begin{align*} R_n &= \frac{1}{n} f\left(\frac{1}{n}\right) + \frac{1}{n} f\left(\frac{2}{n}\right) + \cdots + \frac{1}{n} f\left(\frac{n}{n}\right) \\ &= \frac{1}{n} \left(\frac{1}{n}\right)^2 + \frac{1}{n} \left(\frac{2}{n}\right)^2 + \cdots + \frac{1}{n} \left(\frac{n}{n}\right)^2 \\ &= \frac{1}{n}\cdot\frac{1}{n^2}(1^2 + 2^2 + \cdots + n^2) \\ &= \frac{1}{n^3}(1^2 + 2^2 + \cdots + n^2). \end{align*} $$ Použitím výše uvedeného vzorce dostaneme: $$ R_n = \frac{1}{n^3}\cdot\frac{n(n+1)(2n+1)}{6} = \frac{(n+1)(2n+1)}{6n^2}. $$ Potom přechodem k limitě dostaneme: \begin{align*} \lim_{n \to \infty} R_n &= \lim_{n \to \infty} \frac{(n+1)(2n+1)}{6n^2} \\ &= \lim_{n \to \infty} \frac{1}{6}\left(\frac{n+1}{n}\right) \left(\frac{2n+1}{n}\right) \\ &= \frac{1}{6}\cdot\lim_{n \to \infty}\left(1 + \frac{1}{n}\right) \cdot\left(2 + \frac{1}{n}\right) \\ &= \frac{1}{6}\cdot 1\cdot 1\cdot 2 = \frac{1}{3}. \end{align*} Nyní dává smysl definovat obsah $A$ obrazce $S$ jako limitu: $$ A = \lim_{n \to \infty} R_n = \lim_{n \to \infty} L_n = \frac{1}{3}. $$

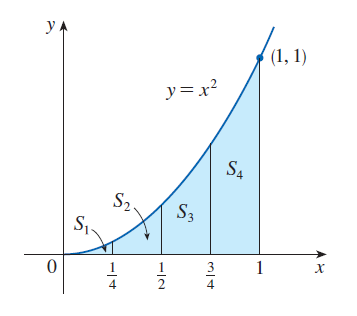
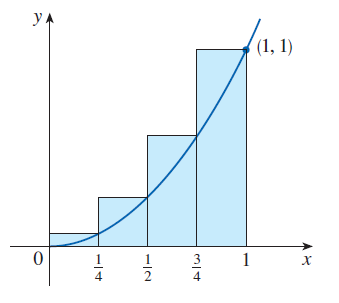
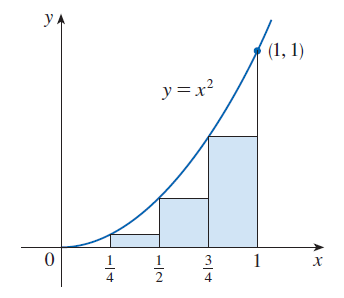
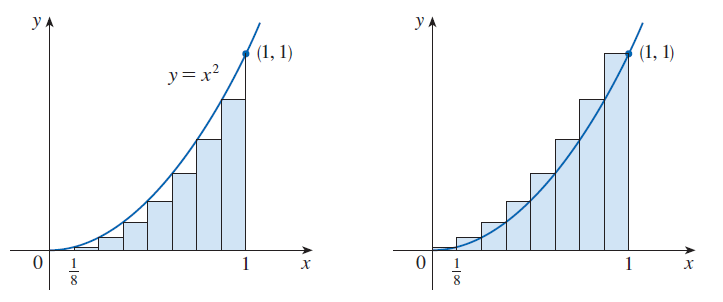
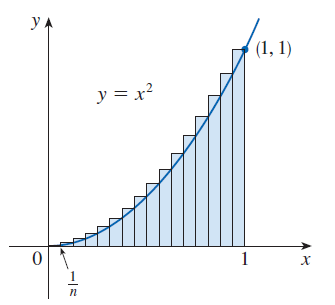
Zobecnění předchozího příkladu

Nyní uvažujme nezápornou spojitou funkci $f:\langle a,b \rangle \to \mathbb{R}_0^+$ a uvažujme obrazec $S$ ohraničený grafem funkce $f$, osou $x$ a přímkami $x = a$ a $x = b$. Viz následující obrázek:

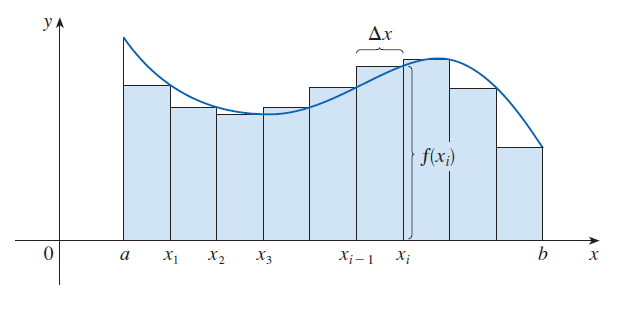
Rozdělme obrazec $S$ na $n$ částí $S_1, S_2, \ldots, S_n$ nad dílčími intervaly $⟨x_{i-1}, x_i⟩$ mající konsntní délku $\Delta x = \frac{b-a}{n}$. Šířka každého dílčího pruhu $S_i$ je tedy rovna $\Delta x$. Dílčími intervaly jsou intervaly: $$ \langle x_0, x_1 \rangle,\ \langle x_1, x_2 \rangle,\ \ldots,\ \langle x_{n-1}, x_n \rangle, $$ kde $x_0 = a$ a $x_n = b$. Pravé koncové body dílčích intervalů jsou: $$ \begin{align*} x_1 &= a + \Delta x, \\ x_2 &= a + 2\Delta x, \\ x_3 &= a + 3\Delta x, \\ &\vdots \\ x_{n-1} &= a + (n-1)\Delta x, \\ x_n &= a + n\Delta x = b. \end{align*} $$ Obecně $x_i = a + i\Delta x$. Obsah každého dílčího obrazce aproximujeme obsahem obdélníku, jehož základna má délku $\Delta x$ a výška je rovna funkční hodnotě funkce $f(x_i)$ v pravém koncovém bodě příslušného dílčího intervalu. Obsah $i$-tého dílčího obdélníku je tedy roven: $$ f(x_i)\Delta x. $$ Konečně obsah obrazce $S$ budeme aproximovat součtem $R$ obsahů dílčích obdélníků: $$ R_n = f(x_1)\Delta x + f(x_2)\Delta x + \cdots + f(x_n)\Delta x = \sum_{i=1}^n f(x_i)\Delta x. $$ Viz následující obrázek:

Uveďme nyní definici obsahu obrazce $S$.

Definice: Obsah $A$ obrazce $S$ ohraničeného grafem funkce $f$, osou $x$ a přímkami $x = a$ a $x = b$ je roven: $$ \boxed{ A = \lim_{n \to \infty} R_n = \lim_{n \to \infty} [f(x_1)\Delta x + f(x_2)\Delta x + \cdots + f(x_n)\Delta x]. } $$

Poznámky:

Je možné ukázat, že díky předpokladu spojitosti funkce $f$ na intervalu $⟨a,b⟩$ limita $\lim_{n\to∞} R_n$ vždy existuje.
Lze též ukázat, že pokud použijeme levé koncové body dílčích intervalů, potom $$ A = \lim_{n\to∞} L_n = \lim_{n\to∞} [f(x_0)Δx + f(x_1)Δx + \cdots+ f(x_{n - 1})Δx]. $$
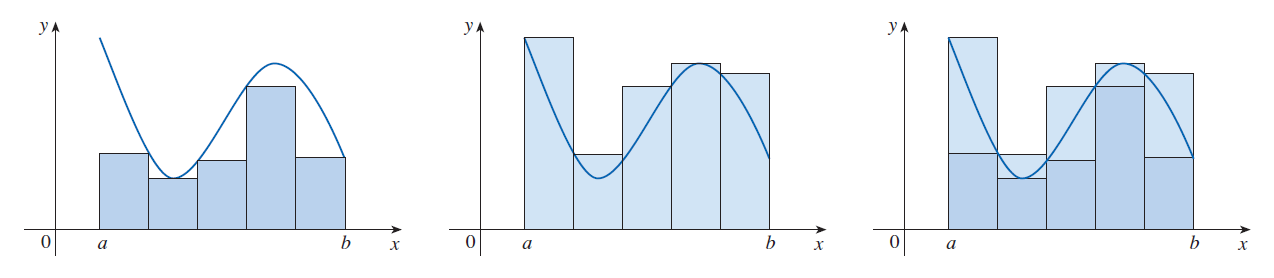
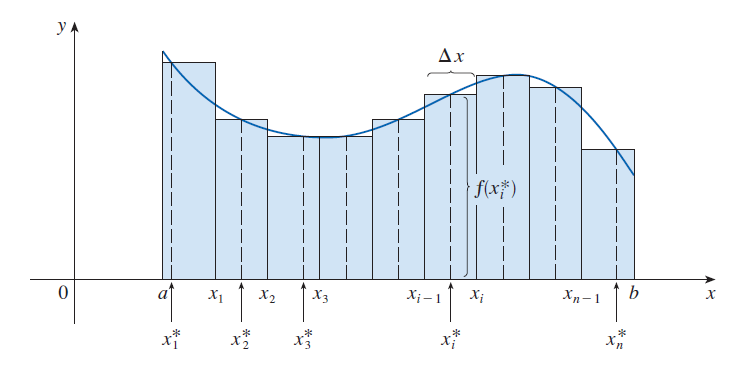
Místo levých resp. pravých koncových bodů můžeme vybrat body $x_1^*,\ x_2^*,\ldots,x_n^*,$ kde pro každé $i$ je $x_i^* ∈ ⟨x_{i-1}, x_i⟩.$ Potom lze obsah $A$ obrazce $S$ vyjádřit pomocí obecnější limity: $$ A = \lim_{n\to∞} [f(x_1^*)Δx + f(x_2^*)Δx + \cdots+ f(x_n^*)Δx] =\lim_{n\to\infty} \left[\sum_{i=1}^nf(x_i^*) \Delta x\right]. $$ Viz obrázek dole.
Vzhledem ke spojitosti funkce $f$ na každém z dílčích intervalů lze pro každé $i$ volit výběrový bod $x_i^* ∈ ⟨x_{i-1}, x_i⟩$ tak, že $f(x_i^*) = \min_{x ∈ ⟨x_{i-1}, x_i⟩} f(x).$ Dostaneme tak tzv. dolní integrální součet, který je dolním odhadem obsahu $A$. Analogicky lze definovat horní integrální součet, který je horním odhadem obsahu $A$ obrazce $S.$

Ekvivalentní definice obsahu obrazce: Obsah obrazce $S$ je jednoznačně definovaná hodnota $A$, větší než livolný dolní integrální součet a menší než libovolný horní integrální součet.

Program, který počítá Riemannův integrální součet pro zadanou funkci $f(x)$ na intervalu $⟨a,b⟩$ a zadaný počet dílčích intervalů $n$ je k dispozici na adrese: zde.

Příklad: Nechť $A$ označuje obsah obrazce omehčeného grafem funkce $f(x) = e^{-x}$ a přímkami $x = 0$ a $x = 2.$

Vyjádřeme $A$ jako limitu integrálních součtů a kde výběrové body budou pravé koncové body dílčích intervalů. Tuto limitu nepočítejme.
Odhadněme $A$ pomocí Riemannova integrálního součtu, kde výběrové body budou středy dílčích intervalů. Použijme 10 dílčích intervalů.

Řešení:

$A = \int_0^2 e^{-x}dx = \lim_{n\to\infty} \sum_{i=1}^n e^{-x_i}\Delta x_i,$ kde $x_i^* = \frac{2i}{n}$, $\Delta x_i = \frac{2}{n},$ $i = 1, 2,\ldots,n.$ Nyní dosaďme $\frac{2i}{n}$ za $x_i$ ve výše uvedené sumě: \[ A = \lim_{n\to\infty} \sum_{i=1}^n e^{-\frac{2i}{n}}\cdot\frac{2}{n}. \] Poslední sumu rozepišme: \[ = \lim_{n\to\infty} \left[e^{-\frac{2}{n}}\cdot\frac{2}{n} + e^{-\frac{4}{n}}\cdot\frac{2}{n} + \cdots + e^{-\frac{2n}{n}}\cdot\frac{2}{n}\right]. \] Po úpravě dostaneme: \[ = \lim_{n\to\infty} \frac{2}{n}\left[e^{-\frac{2}{n}} + e^{-\frac{4}{n}} + \cdots + e^{-2}\right]. 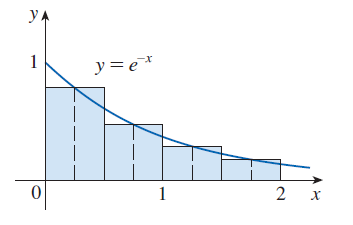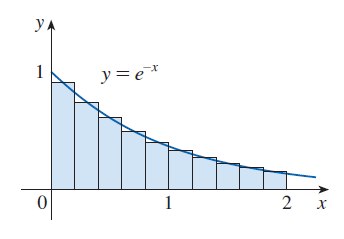\] Na obrázku níže je zobrazen graf funkce $f(x) = e^{-x}$ na intervalu $⟨0,2⟩$ pro 4 dílčí intervaly.
Vyčíslemem Riemannův integrální součet pro 10 dílčích intervalů, kde výběrové body budou tentokrát středy dílčích intervalů. $\Delta x = \frac{2}{10} = 0.2$ a $x_i = 0.2i$ pro $i = 0, 1, \ldots, 10$. Pak pro každé $i$ je $x_i^* = \frac{x_{i-1} + x_i}{2} = \frac{0.2(i-1) + 0.2i}{2} = 0.2i - 0.1$ pro $i = 1, 2, \ldots, 10$. Tedy \[ \begin{align*} M_{10} &= \sum_{i=1}^{10} f(x_i^*)\Delta x_i = f(0.1)\Delta x + f(0.3)\Delta x + \cdots + f(1.9)\Delta x \\ &= e^{-0.1}\cdot0.2 + e^{-0.3}\cdot0.2 + \cdots + e^{-1.9}\cdot0.2\approx 0.8632. \end{align*} \]

Určitý integrál

Úvod

Definice. Nechť $f$ je funkce definovaná na intervalu $⟨a,b⟩$. Dále uvažujme dělení intervalu $⟨a,b⟩$ na $n$ dílčích intervalů $⟨x_{i-1}, x_i⟩$ o konstantní délce $\Delta x = \frac{b-a}{n}$. Dělícími body budou potom body $x_0 = a,\ x_1 = a + \Delta x,\ x_2 = a + 2\Delta x,\ \ldots,\ x_n = b$. Nechť pro každé $i = 1, 2, \ldots, n$ je $x_i^* ∈ ⟨x_{i-1}, x_i⟩$. Potom budeme definovat určitý integrál funkce $f$ na intervalu $⟨a,b⟩$ jako limitu: \[ \boxed{ \int_a^b f(x)dx = \lim_{n\to\infty} \sum_{i=1}^n f(x_i^*)\Delta x} \] za předpokladu, že tato limita existuje a nezávisí na volbě výběrových bodů $x_i^*.$ Potom též říkáme, že funkce $f$ je integrovatelná na intervalu $⟨a,b⟩$ nebo že funkce $f$ má na intervalu $⟨a,b⟩$ Riemannův integrál.